今日題目

題目連結：1863. Sum of All Subset XOR Totals
題目主題：Array, Backtracking, Bit Manipulation

雖然昨天的題目也有提到 Bit ，不過實作時其實不太需要用到相關知識，今天的題目在實作時會用到相關知識，所以會分享一下關於 Bit 的基本概念。

簡單說說 Bit

Bit 又稱為二進制，簡單說的話 Bit 會看到的數字不是 1 就是 0，通常我們平常看到的數字是十進制，最基本的概念是需要了解如何將十進制轉成二進制，先看這張表：

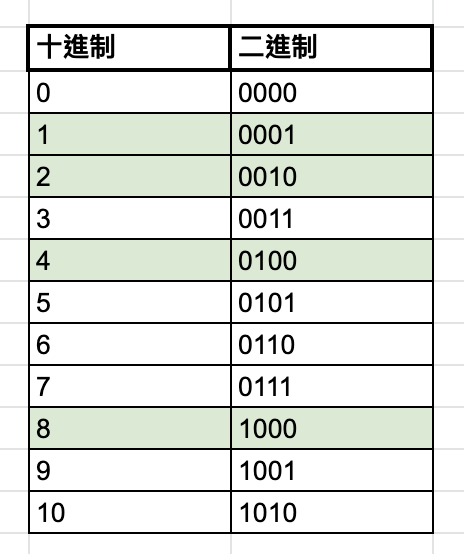
先從綠色的部份開始看，1 是2的零次方，2 是2的1次方，基本上二進制裡面 1 每往左走一格就是多一個次方，例如 100000 就是 2的 6 次方，轉成 10 進制就是 32。

如果要用二進制表示十進制的 3 或 5 會怎麼看？用 3 當例子是 0011，只要把 1 拆開來看就很好理解，拆開來會變成 0010 跟 0001 那就是 2 跟 1，加起來就是 3。

Bit 邏輯運算

這邊介紹幾種基本的 Bit 邏輯運算：

1. AND
   範例： 3 AND 5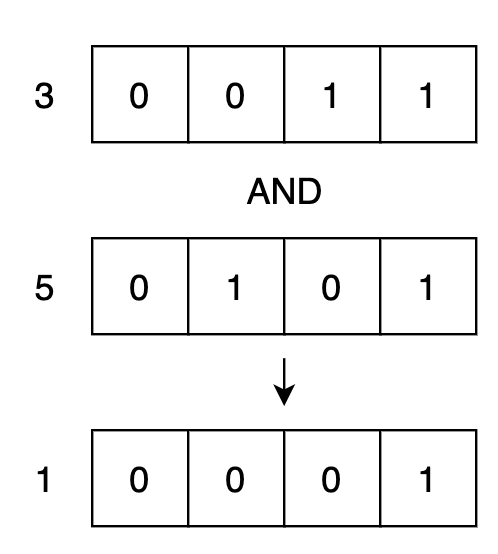
   
   上圖中可以看到這樣運算出來結果是0001，當兩個數字轉成二進制以後，同樣位置出現 1 ，就會繼續將 1 保留到下面，其他都轉成 0。

2. OR
   範例： 3 OR 5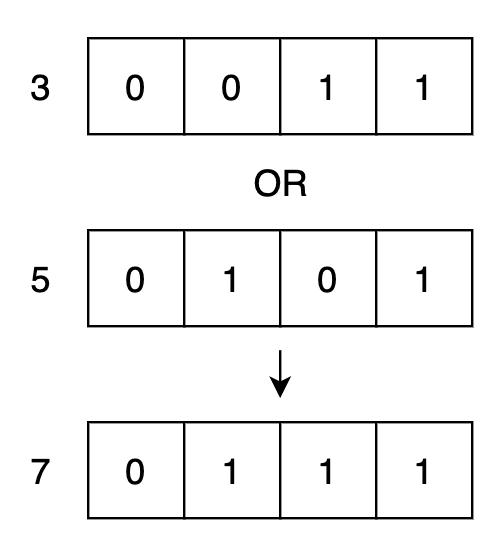
   
   上圖中可以看到這樣運算出來結果是0111，當兩個數字轉成二進制以後，只要兩個數字其中一個位置有 1，就會繼續將 1 保留到下面，其他都保持 0。

3. XOR
   範例： 3 XOR 5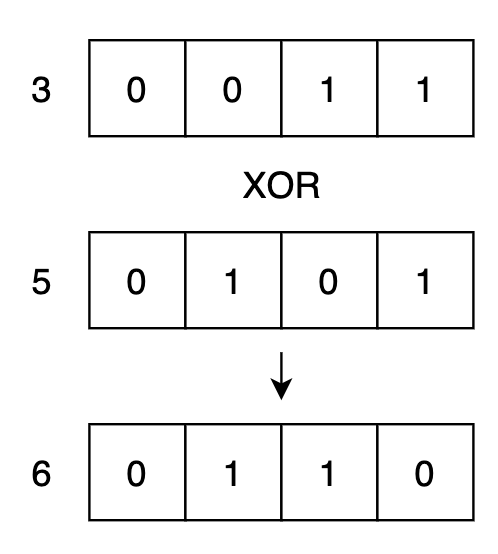
   
   上圖中可以看到這樣運算出來結果是0110，當兩個數字轉成二進制以後，同樣位置出現 1 ，會將數字改為 0 放到下面，其他只要其中一個有 1 就保留到下面。

題目解說

建議可以看看LeetCode原本的題目說明，這邊是用我的方式說明題目，參考就好。

題目會給一個數字陣列，目的是將這個陣列中的所有子集合的 XOR 總和加總後回傳。

Ex. [2, 5, 6]的XOR總和等於 1，2 XOR 5 XOR 6 運算過程如下：

1. 2 XOR 5 = 7 看成二進制如右 010 XOR 101 = 111。
2. 111 二進制轉成十進制是 7。
3. 7 XOR 6 = 1 看成二進制如右 111 XOR 110 = 001。
4. 最後 001 二進制轉十進制是 1。

約束：

• 1 <= nums.length <= 12
• 1 <= nums[i] <= 20

範例1

輸入: nums = [1,3]
輸出: 6
解說: [1,3] 總共會有四個子集如下:
- 空的子集總和就是 0。
- [1] 只有一個數字總和直接是 1。
- [3] 只有一個數字總和直接是 3。
- [1,3] 1 XOR 3 = 2, 看成二進制 01 XOR 11 = 10，10 二進制轉十進制等於 2。
最後加總 -> 0 + 1 + 3 + 2 = 6

範例2:

輸入: nums = [5,1,6]
輸出: 28
解說: [5,1,6] 總共會有四個子集如下:
- 空的子集總和就是 0
- [5] 只有一個數字總和直接是 5.
- [1] 只有一個數字總和直接是 1.
- [6] 只有一個數字總和直接是 6.
- [5,1] 5 XOR 1 = 4, 看成二進制 101 XOR 001 = 100，100 二進制轉十進制等於 4。
- [5,6] 5 XOR 6 = 3, 看成二進制 101 XOR 110 = 011，011 二進制轉十進制等於 3。
- [1,6] 1 XOR 6 = 7, 看成二進制 001 XOR 110 = 111，111 二進制轉十進制等於 7。
- [5,1,6] 5 XOR 1 XOR 6 = 2. 看成二進制 101 XOR 001 XOR 110 = 010，010 二進制轉十進制等於 2。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

範例3

輸入: nums = [3,4,5,6,7,8]
輸出: 480

建議到這邊先停下來，嘗試自己解解看，若沒有想法可再繼續走下去。

解題的想像

文字描述

1. 寫一個遞迴方法傳入以下：
   • 目標陣列
   • 目前總和
   • stack 存放要計算的子集合
2. 進入遞迴方法：
   • 將 stack 目前的子集計算XOR總和，加至目前總和
   • 跑一個for迴圈繼續計算所有子集
3. 最終遞迴方法會回傳所有子集的XOR總和的加總。

圖解過程

範例：[3, 4, 5, 6, 7]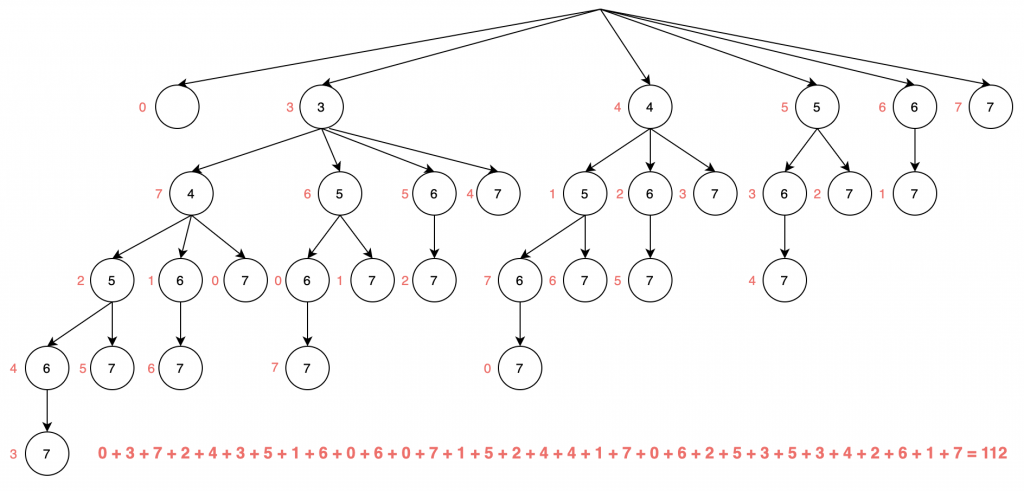

上圖中，每一個節點都是一個子集合，越下層代表這個子集是越多值組成的，如最左邊最下面的 7 是從最上面的 3 走下來的，這個子集合為 [3, 4, 5, 6, 7]。而中間的 4 -> 5 -> 6 -> 7 就代表 [4, 5, 6, 7]，最上面的 3 這個節點就代表 [3] 這個子集合，最後一個例子可以看到最左上角有一個空的代表空的子集合，如同前面範例空的子集也會算在裡面。

再來看看每個節點左邊的紅色數字，代表這個子集合的XOR總和，建議各位也可以跟著都算一次，會更清楚每個算出來的結果是怎麼來的。

最後可以看到下面的紅色加總，就是將所有子集合的XOR總和的加總，這個範例得到的結果會是 112。

若因為沒想法而走到這邊，建議看完想像以後再給自己一次機會試一次。

程式碼撰寫

class Solution:
    def total(self, nums, index = 0, sumValue = 0, stack = []):
        # 將目前的子集合加總
        tmpValue = 0
        for value in stack:
            tmpValue ^= value
        sumValue += tmpValue
        
        # 找出所有子集合
        for i in range(index, len(nums)):
            stack.append(nums[i])
            sumValue = self.total(nums, i+1, sumValue, stack) 
            stack.pop()
    
        # 回傳目前總和
        return sumValue
    
    def subsetXORSum(self, nums: List[int]) -> int:
        return self.total(nums)

希望您今天能瞭解到...

1. Bit 基本概念
2. 1863. Sum of All Subset XOR Totals 的解題方法

若內容有什麼問題或建議歡迎一起交流：）
感謝您今天願意花時間看完這篇文章~~~~

Next：1974. Minimum Time to Type Word Using Special Typewriter